题目概述
本次作业主要解决了对一个输入表达式的化简问题,三次作业中不断增加输入表达式的复杂程度。
Unit 1
本次作业需要完成的任务为:读入一个包含加、减、乘、乘方以及括号(其中括号的深度至多为 1 层)的单变量表达式,输出恒等变形展开所有括号后的表达式。
在本次作业中,展开所有括号的定义是:对原输入表达式进行恒等变形,且新表达式不包含(和)。
eg:(x+1)^3+1 -> x^3+3*x^2+3*x+2
架构设计
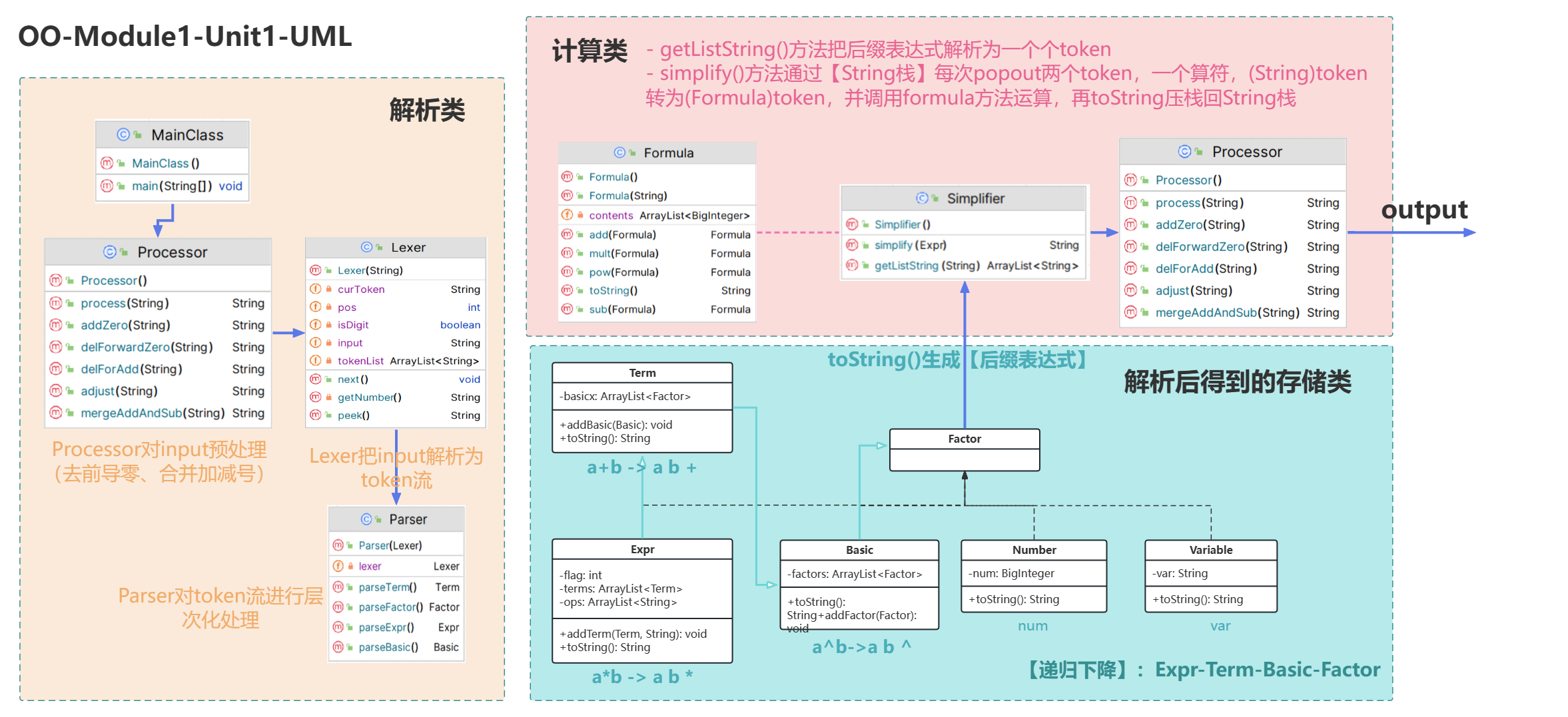
主要思路由training得到,
1.先对输入表达式通过递归下降法生成后缀表达式:思路主要来自于一位学长的博客:Tan‘s blog
2.再通过栈的方法对后缀表达式进行计算与化简。具体而言,通过空格将后缀表达式分割为字符串数组;再按后缀表达式计算的原则,按顺序将非符号式子压入栈中,遇到符号弹出最近的两个式子进行计算,再压入栈中。
String suffix = expr.toString();//后缀表达式
ArrayList<String> suffixs = getListString(suffix);
Stack<Formula> stack = new Stack<>();
在这里会涉及到String和Formula的转换,为此我写了一个从String构造Formula的构造方法,实现了由数字、x两个基本项构造Formula。这是因为在本单元得到的后缀表达式中,单项要么是数字,要么是x。而后面更复杂的多项则由Formula的计算方法得到即可。
public class Formula {
//private HashMap<BigInteger, BigInteger> contents;//a * x ^ b,即为<b,a>,因为b是key,一个指数对应唯一的一个系数
private ArrayList<BigInteger> contents;
public Formula(String content)
{
contents = new ArrayList<>();
if (content.matches("\\d+")) {
contents.add(new BigInteger(content));//0---content
//contents.put(new BigInteger("0"), new BigInteger(content));//x的0次方
}
else if (content.matches("x")) {
contents.add(BigInteger.valueOf(0));
contents.add(BigInteger.valueOf(1));
//contents.put(new BigInteger("1"), new BigInteger("1"));
}
}
}
当然,也需要实现最后Formula.toString()方法输出最终式子。
值得一提的是,第一单元中计算类Formula中的存储结构是**ArrayList<BigInteger>**,数组的第i项表示x的i次方所对应的系数。这一数据结构在只有x的多次方相加时很有用。(感谢syc的思路!)但是,在之后更复杂的单项式情况中,就要考虑别的数据结构了。
度量分析

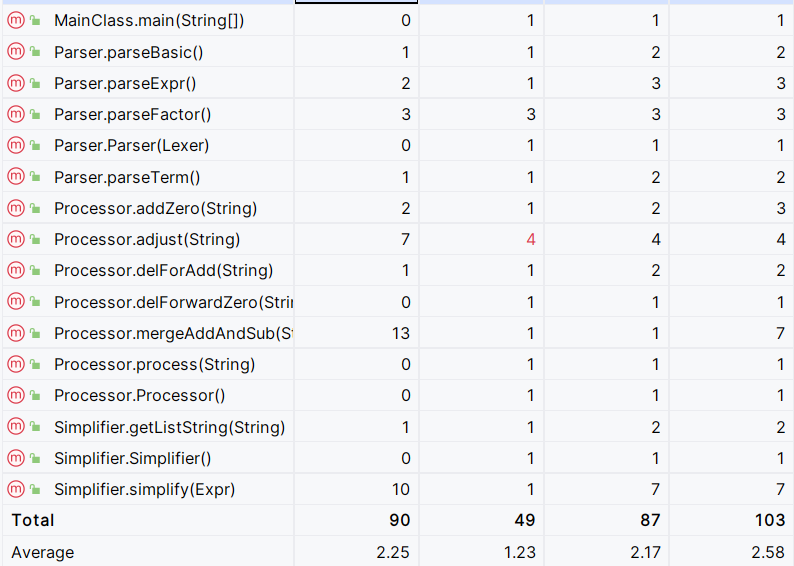 高复杂度主要集中于三个类:化简输入表达式的Processor、用于计算的Formula、用于栈计算后缀表达式的Simplifier。其中,Formula.toString(),Processor.mergeAddAndSub()都是由于字符串处理而导致的高复杂度。Simplifier.simplify()是因为对不同符号要进行分类讨论。
高复杂度主要集中于三个类:化简输入表达式的Processor、用于计算的Formula、用于栈计算后缀表达式的Simplifier。其中,Formula.toString(),Processor.mergeAddAndSub()都是由于字符串处理而导致的高复杂度。Simplifier.simplify()是因为对不同符号要进行分类讨论。
bug分析
在中测、强测和互测中,第一次作业都没有出现bug。在针对中测数据的debug上我花了4个小时的时间。出现的bug种类繁多,主要是因为我在各个类中都会存在细小的疏忽。经过这一周的debug,我认识到进行单元测试——每写完一个函数测一个函数的重要性。
Unit 2
本次作业在第一单元的基础上,新增了指数函数和自定义函数两类,需要实现更复杂的化简。
架构设计
一开始,我想要继续复用上一周的思路,即生成后缀表达式再进行解析。在生成后缀表达式这一步的思路我比较清晰,可是如何从后缀表达式计算得到最终结果,我想了三天没有得出最终结果……周六晚八像洪水猛兽一样袭来,没有思路的我最终选择了浩浩荡荡的大重构。(此处特别感谢zhw&wyt的帮助!楼梯间讲架构/新主二楼&五教楼梯口的陪伴都很浪漫!)
重构的思路即主流架构思路。将数据存储与计算类从一个单独的类变成两个类:Poly和Mono。Poly为多项式,Mono为单项式,Mono的属性包含coef(BigInteger)、index(BigInteger)、exponent(Poly),表示coef*x^index*exp(exponent)。每一个数据解析类(如Expr、Term、各种Factor)书写**toPoly()**方法,再通过Poly和Mono的计算方法计算得到最终结果。
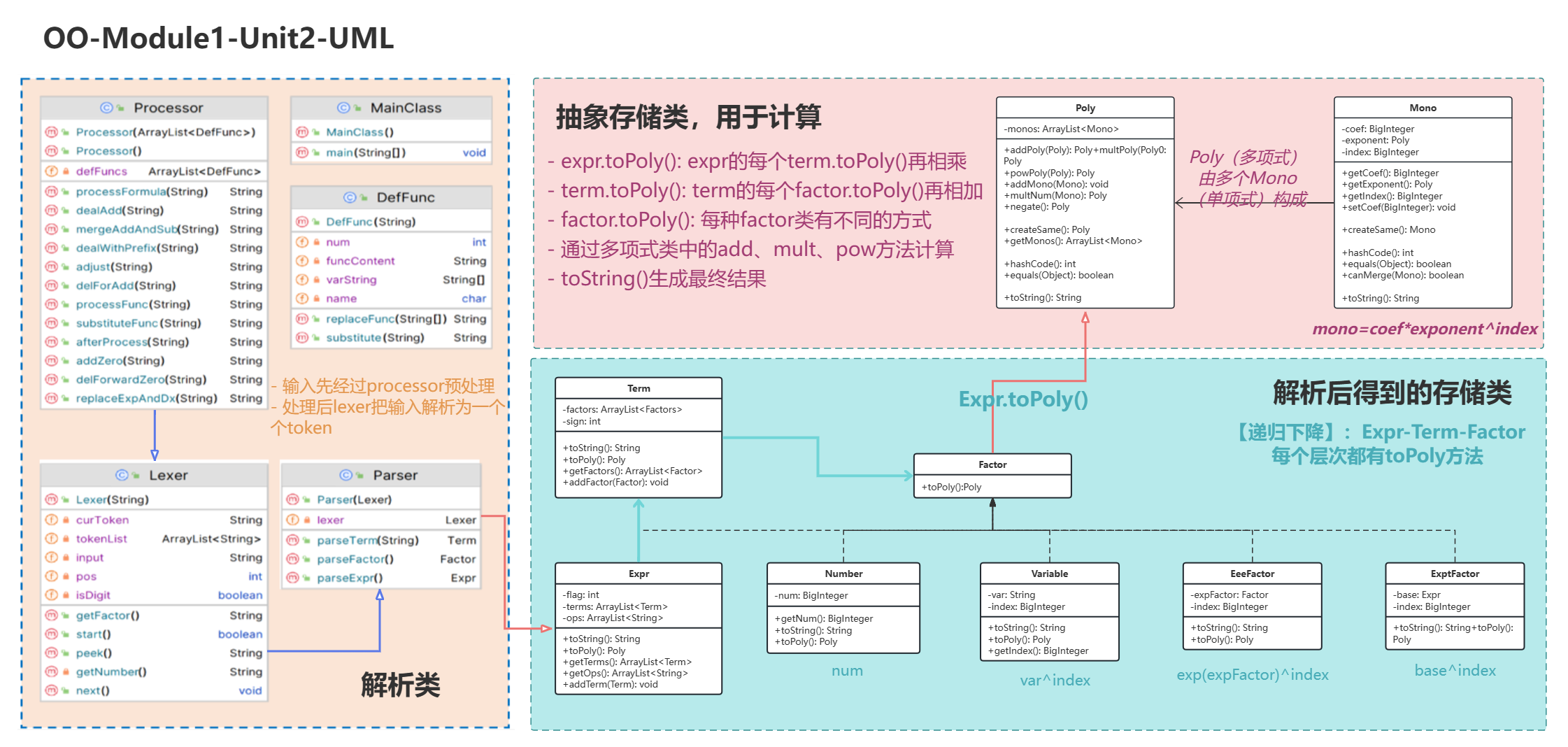
值得注意的是,在有关自定义函数的处理部分我也思考了很久,最后在zhw的帮助下写出了一个比较好的字符串替换思路:对输入字符串进行反复扫描,替换其中的自定义函数。具体的替换方法写在自定义函数类DefFunc中,通过左括号加右括号减的count和,判断是否进行字符串分割。
public String substituteFunc(String str) {
String s = str;
while (s.contains("f") | s.contains("g") | s.contains("h")) {
for (DefFunc defFunc : defFuncs) {
s = defFunc.substitute(s);
}
}
return s;
}
在第四周的研讨课中,同组的trj同学提出了一个让我很受教的方法,即对象替换处理自定义函数。具体方法如下:
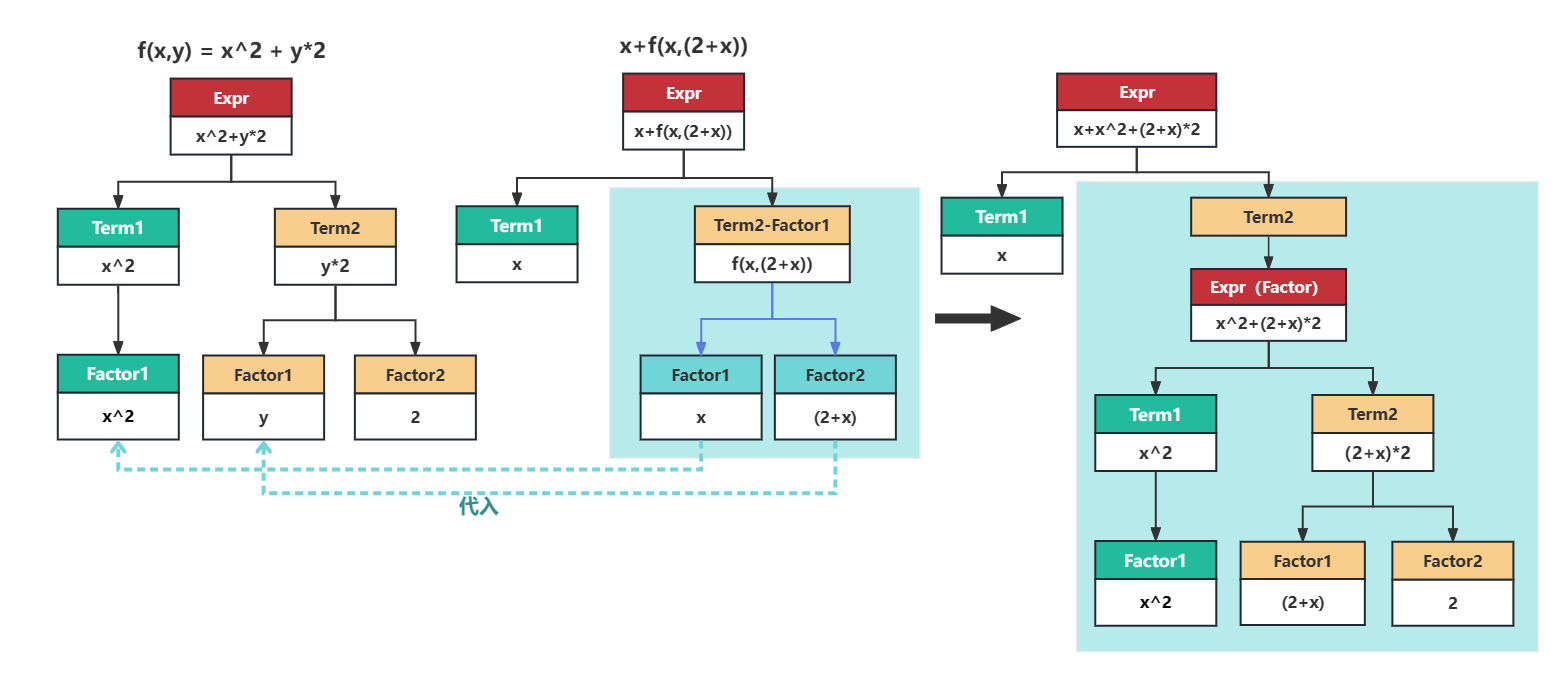
在输入自定义函数表达式时,使用递归下降法对其进行解析,得到自定义函数语法树,它的底层是不同名字的varFactor。再输入待处理表达式,依然使用递归下降法对其进行解析,若遇到函数名,用parseFactor()方法得到它的每一个实参Factor(具体parse的次数由函数名对应的形参数量而决定);再将所得到的实参Factor替换给自定义函数语法树底层的varFactor,得到替换后的新自定义函数语法树,将语法树最高层的Expr返回作为一个Factor。
度量分析
(仅列出复杂度较高的几个方法)
| method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| DefFunc.substitute(String) | 16.0 | 4.0 | 8.0 | 9.0 |
| Parser.parseFactor() | 10.0 | 4.0 | 7.0 | 7.0 |
| Poly.addPoly(Poly) | 8.0 | 4.0 | 5.0 | 5.0 |
| Poly.multPoly(Poly) | 11.0 | 1.0 | 9.0 | 9.0 |
| Poly.toString() | 17.0 | 6.0 | 9.0 | 12.0 |
| Processor.dealWithPrefix(String) | 9.0 | 1.0 | 10.0 | 10.0 |
复杂度高的方法包含Processor处理负号前缀、函数替代、parseFactor、Poly的计算与toString()。这些方法中,基本都有比较复杂的分类讨论情况以求面面俱到。
bug分析
在第二次作业中,由于重构的原因写出来的bug更更多了,大概de了惊人的8个小时……(常常觉得自己有写bug的天赋)下面按照发现的顺序记录一下。
| 序号 | 输入数据 | 错误原因 |
|---|---|---|
| 1 | 1 // f(x) = x^6 // f(x^2) | 自定义函数字符串替换时,没有给每一项因子都加括号导致出现x^2^6无法解析。 |
| 2 | 1 // f(y)=y^2 // (f(exp(x)))^2+1 | 为了减少输出长度,在第一次作业中会找到式子里的第一个加号,把加号后面的东西和前面的东西顺序交换。第二次并没有改变这个思路,但是由于exp((2+x))这样的形式出现,复用这种优化思路会导致x))exp((2的搞笑输出。 |
| 3 | 3*(((e(x))*((e(x))+(e(x)))))^2+x | parser的解析中,有关e,多了一个lexer.next(),跳过了)的同时也跳过了后面的数 |
| 4 | 0 // (e(x)+2*e(x))^2 | 进行Poly的计算时,用的是浅拷贝,即没有新建一个和参与预算数一样的Poly,直接把参与预算数给修改了。解决方案:加入深拷贝方法createSame(),Poly和Mono类都需要。 |
| 5 | 0 // exp(-1)或者exp(-x) | 复用了第一次作业中Processor的一个加零方法:假如是首项且为负号,那么变成“0-”,从而方便解析。如:(-x)->(0-x)。但是,在第二次作业中这样做会使exp内部不再是表达式因子。解决方法:1.改变lexer方法使得负数也被看成一个lexer;2.识别到exp之后,不再parseFactor,而直接parseExpr,从而不需要这个加零方法。(感谢bzh同学的思路)p.s.在明白其实可以直接parseExpr之前,我执着地使用parseFactor并认为需要给exp()再加一个括号。因为一直没想出来该怎么只给exp加括号,所以摆烂地直接把每个括号都变成了两个括号,从而导致强测的一个点出现超时。:((、、越想越好笑……) |
在互测hack别人的代码时,我所在的房间大家的主要问题都是过度优化,比如把exp(-x)当成合法的。
而我在强测中WA-2,TLE-1,互测中WA-2。出现的错误如下:
| 序号 | 输入数据 | 错误原因 |
|---|---|---|
| 1 | - | TLE,倍增括号导致的过度嵌套。上表的第五点已提及。 |
| 2 | 3 // f(z, y)=+ +(-y)^01-exp(z )y^ +002 10 // g (x ,z ,y) =-(+y^ +04 +- 19 ) * y–+0014exp( exp(+02)) // h (x,y, z)=– 0013y^03–(+(++exp(z ) ^+2+ z^+2*(y^+3*-0015*+014 + z* y^ +01 +x ^ +000)^2 ))^005+-z ^+003 // + (f ( exp(017)^+002,(x^+1 x^+04x^+001+x^+1x^01 ) ^+1)-( -x-+( x^04 – +5x^+001x^ +005)^+000exp(x^02)^2)^002 ) | 两个强测的WA都是这个bug。漫长的debug后发现在函数替换步骤中出现问题。具体的错误在预处理Processor中出现,先mergeAddandSub(合并连续加减号&去掉空格)再subFunc(把自定义函数替代进来)就不会出错,反之会出错……最关键的错误数据是f (x)。其实是因为预先没有去掉空格的时候,funPos指向’f‘,但funPos+2指向的位置不是’(‘后的x,而是前面的那一堆空格。substring(funPos+2会得到一个有前括号的奇怪实参。(在这个例子里就是:“(x”会作为一个实参来进行下一步替换。) |
| 3 | 0 // -x-1-exp(x) | 两个互测的WA点都是这个bug。这个点的错误原因是,按照我的lexer逻辑,“+”是划分token的分界线,所以“-x-1-exp”会被当成一个token。在思考后我没有改变lexer的逻辑,而是把每一个“因子-因子”的格式都改成了“因子+-因子”,从而解决了这个问题。 |
优化
由于重构得实在心力交瘁,第二次作业的优化我完全没做。甚至连基本的合并同类项,都因为**只重写了Poly.equals()没重写Mono.equals()**而没有实现。结果就是,在debug的过程中有一些眼睛疲惫……所以还是要先把基础的优化做好,磨刀不误砍柴工。
Unit 3
在第一次作业基础上,本次迭代作业增加了以下几点:
- 本次作业支持求导操作,新增求导算子 。
- 求导因子可以出现在很多位置,包括函数调用实参,指数函数内部等,注意考虑周全。
- 为了限制难度,在输入中,求导算子不会在自定义函数中出现。
- 本次作业函数表达式中支持调用其他“已定义的”函数(保证不会出现递归调用)。
架构设计
感谢上一周血与泪中的重构!这一周总算轻松一些了。
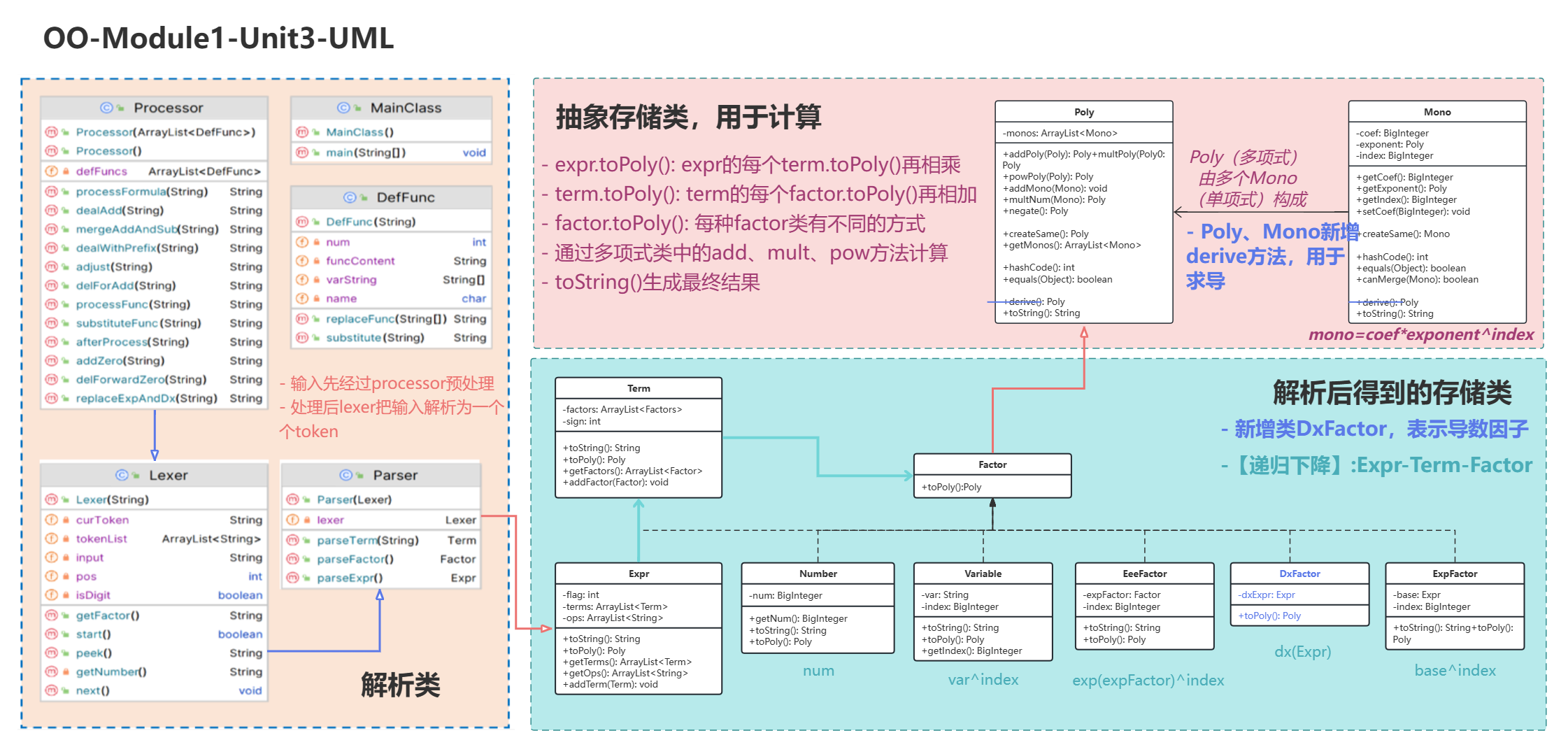
针对自定义函数的递归调用,原有的字符串替换不会发生问题,所以没有更改。
针对求导因子的出现,新增类DxFactor,存储dx()中的表达式。Poly、Mono新增derive()方法,用于DxFactor.toPoly()时的求导。具体而言,Poly.derive()即求出其中每一个Mono.derive()之和,而Mono.derive()则遵循基本的求导法则即可。
度量分析
(仅列出复杂度较高的几个方法)
| method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| DefFunc.substitute(String) | 16.0 | 4.0 | 8.0 | 9.0 |
| Parser.parseFactor() | 11.0 | 5.0 | 8.0 | 8.0 |
| Processor.mergeAddAndSub(String) | 13.0 | 1.0 | 1.0 | 7.0 |
| Poly.addPoly(Poly) | 8.0 | 4.0 | 5.0 | 5.0 |
| Poly.multPoly(Poly) | 11.0 | 1.0 | 9.0 | 9.0 |
| Poly.toString() | 8.0 | 3.0 | 4.0 | 7.0 |
| Mono.toString() | 38.0 | 18.0 | 26.0 | 28.0 |
| Processor.dealWithPrefix(String) | 9.0 | 1.0 | 12.0 | 12.0 |
可以看出,对比起上一周的作业,原有的高复杂度方法依然在列。不同的是,我调整了Poly的toString()方法,将其中的大部分特判输出放入了Mono.toString()中,造成了这个方法的超高复杂度。
bug分析
这一次作业中,我在中测和强测中均未出现bug。在针对中测的debug中,曾经出现过嵌套dx的问题:dx(x-dx(x))。最后发现和第二次互测错误的点一模一样,没有特判dx也是需要添加“+”作为分隔符的一种类型,将原式转化为x+-dx(x),从而导致x-dx(x)在lexer阶段被解析为一个token。
追根溯源,产生这个bug的方法是Processor.dealAdd(String),这个方法复杂度并不高,但是作为预处理的一部分容易被忽视。下次迭代时还是应该顺着预处理每一步的思路思考需不需要增加东西。
在互测中,发现了两个同学的bug:其中一位在出现嵌套定义自定义函数时会出错,另一位在exp嵌套时会出错。这两个bug也给构造样例提供了思路。
优化
在这一次的作业中,我实现了全部基本的优化。即合并同类项、不输出0、系数为1/0的特判等。
因为没太想清楚提取公因式要怎么做,同时也为正确性感到担忧,我没有做其它的处理。
心得体会
经历过第二周浩浩荡荡的重构,感觉自己第一次对好的架构有了一个深刻的印象。在上学期的oo先导课中,我几乎在重构的边缘线上挣扎了三周,写出了超过300行的main类,最终惊险通过。这一次的重构则让我充分认识到了放弃沉没成本的必要性。
在之后的学习中,我会多练习自己阅读博客的能力。在这一单元的练习中,我发现自己阅读别人博客的能力不太够,即使已经有人写出了很具有参考意义的博客分享,我囫囵吞枣地看过去也不会有什么收获。看博客更像是一个重视质而非量的过程。
最后是对沟通的理解加深了。要更积极地去获取自己想要的思路和方法,去找别人讨论。这对于比较i的我来说确实有些困难……但是值得一试。由衷地感谢在三周迭代中无私帮助我的舍友、同学和助教,再感谢一下自己,总算是闯过了小小的一关。祝我好运~
对第一单元的建议
我觉得非常好。只是希望第二周的研讨课可以提前到周二上,这样可以更好地和同学交流思路,从而产生更好的架构。
「真诚赞赏,手留余香」
真诚赞赏,手留余香
使用微信扫描二维码完成支付
